QUADRATO DI UN BINOMIO

Proviamo a calcolare il quadrato di un binomio, cioè di un polinomio costituito da due monomi. ‘Fare il quadrato’ vuol dire calcolare la potenza di esponente 2 di tale binomio, quindi possiamo procedere come segue:

Proviamo con un altro esempio:

Un ulteriore ultimo esempio:

Osservando la struttura dei risultati possiamo notare che è sempre la stessa:

otteniamo un trinomio in cui due termini sono dati dai quadrati dei termini che compongono il binomio da elevare al quadrato; il terzo termine è il prodotto tra i due termini che compongono il binomio da elevare al quadrato, moltiplicato per 2.

Per esempio, nel primo quadrato di binomio che abbiamo eseguito:

    ,         ,    

Quindi possiamo scrivere le formule:

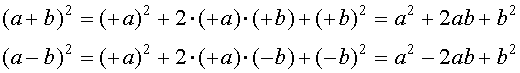
Allora possiamo evitare di fare tutti i passaggi ed applicare subito le formule ottenute, come negli esempi seguenti:

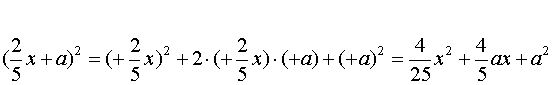
OSSERVAZIONE CONCLUSIVA

Scoprire una struttura nel risultato ci ha permesso di scrivere una formula per calcolare questo prodotto senza fare tutti i passaggi che richiederebbe il prodotto tra polinomi qualunque!

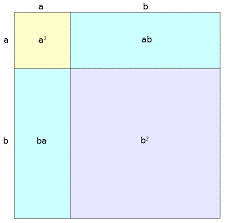
Può essere utile anche una interpretazione di tipo geometrico:

          L’ area del quadrato grande è . Ma se scomponiamo il quadrato come in figura, si ha che l’ area del quadrato grande è la somma di aree parziali date da:

area del quadrato di lato  : 

area del quadrato di lato  :  

area del rettangolo di lati    e     :  

L’ area del rettangolo va contata due volte, quindi in totale avremo proprio:

Ed ecco la videolezione sul Quadrato del binomio
ecco , invece, la playlist con esercizi risolti su quadrati del binomio (anche con frazioni)




Torna alla Home Page