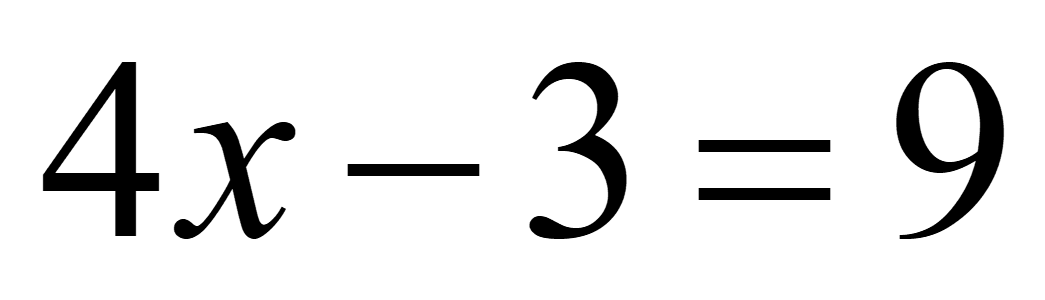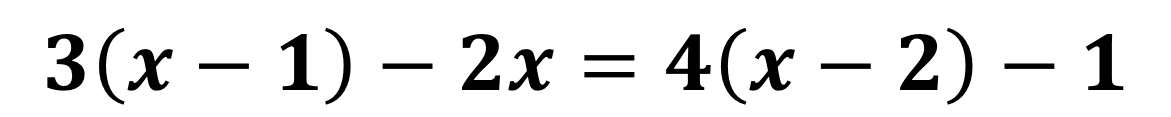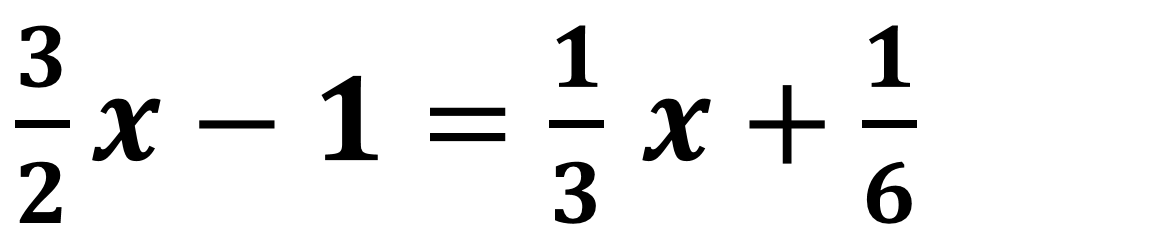Le equazioni numeriche di primo grado in una incognita

Le equazioni che impareremo a risolvere sono equazioni che

ü contengono una sola incognita

ü hanno coefficienti numerici interi o razionali

ü l’ incognita, dopo le dovute semplificazioni, rimane solo elevata al grado1

Cominciamo col dare una definizione importante:

due equazioni si dicono equivalenti quando tutte le soluzioni della prima sono anche soluzioni della seconda e viceversa.

In generale per risolvere un’ equazione si cerca di trasformarla in un’altra ad essa equivalente, ma di forma più semplice.

Per far ciò si utilizzano dei principi, detti principi di equivalenza delle equazioni.

1° principio di equivalenza

“Aggiungendo ad entrambi i membri di   una  equazione lo stesso valore numerico o la stessa espressione algebrica si ottiene una equazione equivalente a quella data”.

è equivalente a

è equivalente a

è equivalente a

è equivalente a

Da questo principio derivano le seguenti regole:

· se uno stesso termine figura in entrambi i membri di un’ equazione può essere soppresso;

· se due termini opposti si trovano nello stesso membro possono essere soppressi;

· si può trasportare un termine di un’ equazione da un membro all’ altro purché gli si cambi il segno (legge del trasporto).

L’ultima regola è quella che utilizzeremo per trasferire tutte le x al primo membro e tutti i termini noti al secondo membro.

2° principio di equivalenza

“Moltiplicando o dividendo entrambi i membri di una equazione algebrica per uno stesso numero diverso da zero , o per una stessa espressione che non si possa annullare, si ottiene una equazione equivalente alla data”.

   è equivalente a     

è equivalente a

Da tale principio derivano le seguenti regole:

· se i due membri di un’ equazione hanno un fattore numerico comune questo può essere soppresso;

· cambiando i segni a tutti i termini di una equazione se ne ottiene un’ altra equivalente;

· moltiplicando (o dividendo) i due membri di una equazione per una espressione, o un numero, conveniente si ottiene un’ equazione equivalente a quella data.

Tale principio si utilizza sia per eliminare denominatori comuni ad entrambi i membri, sia per eliminare il coefficiente (parte numerica) della x al momento di calcolarne il valore finale.

 ,  dividendo entrambi i membri per 2 si ha    ; da cui semplificando si ottiene la soluzione   

Le conseguenze dei due principi ci permettono di risolvere un’ equazione, seguendo i passi che ora indicheremo:

· si eseguono tutte le operazioni presenti nei due membri dell’ equazione;

· si eliminano i denominatori, se vi sono, moltiplicando entrambi i membri per il loro m.c.m.;

· si trasportano tutti i termini che contengono l’ incognita in uno stesso membro e i termini noti nell’ altro cambiando il segno ai termini che vengono spostati (applicazione del 1° principio di equivalenza);

· si riducono i termini simili;

· si dividono il termine incognito e il termine noto per il coefficiente dell’ incognita (applicazione del 2° principio di equivalenza).

ESEMPIO 1:

ESEMPIO 2:

è la soluzione dell’ equazione.

· Può darsi che un’ equazione non ammetta soluzioni, cioè non esista alcun valore dell’ incognita che la verifichi; si dice allora che l’ equazione è impossibile

(il risultato sarà, in tale caso, 0 = ad un numero diverso da 0)

Esempio:  ,    che svolta diventa , e poiché non esiste alcun valore numerico che moltiplicato per 0 dia – 3 come risultato, ciò significa che l’ equazione non ha soluzioni.

· Può darsi che una equazione ammetta un numero illimitato di soluzioni; si dice allora che l’ equazione è indeterminata

(il risultato sarà, in tale caso, sempre 0 = 0)

Esempio:     ,    che svolta diventa     ,

e poiché tutti i numeri moltiplicati per 0 danno come risultato 0, ciò significa che le soluzioni dell’ equazione sono infinite.

Equazioni di primo grado

Torna alla Home Page