Addizione e sottrazione di numeri razionali

Distinguiamo due casi:

Numeri razionali aventi lo stesso denominatore

La somma di due numeri razionali aventi lo stesso denominatore, è un numero razionale avente il denominatore uguale al denominatore dei due operandi e il numeratore uguale alla somma dei numeratori dei due operandi.

Esempio    .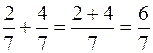

Numeri razionali aventi denominatore diverso

La somma di due numeri razionali aventi denominatori diversi, è un numero razionale avente per denominatore il m.c.m. dei denominatori degli operandi e per numeratore la somma che ha come addendi:

1. Il prodotto del primo numeratore con il quoziente ottenuto dalla divisione del m.c.m. con il primo denominatore;

2. Il prodotto del secondo numeratore con il quoziente ottenuto dalla divisione del m.c.m. con il secondo denominatore;

Esempio: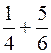

1. Denominatore:  il m.c.m. tra 4 e 6 è 12 , quindi

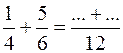
2. Numeratore:

Ø Primo addendo

o Dividiamo il m.c.m. per il primo denominatore:      

o Moltiplichiamo il risultato ottenuto per il primo numeratore:             

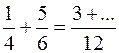
Ø Secondo addendo

o Dividiamo il m.c.m. per il secondo denominatore:          

o Moltiplichiamo il risultato ottenuto per il secondo numeratore:        

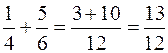
OSSERVAZIONE

E se abbiamo un numero intero?...Facile: 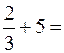 ? Basta osservare che  , quindi

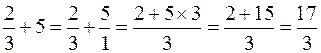
E la sottrazione?

Per la sottrazione si procede nello stesso modo dell’ addizione.

Basta sostituire, nella costruzione del numeratore, la somma con la differenza.

Esempio 1: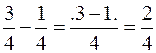               

Esempio 2: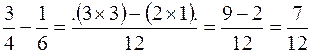              

Esempio 3: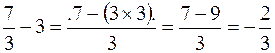     

Esempio 4: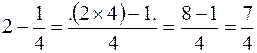                

Torna alla Home Page