COME SI ARRIVA ALLA DEFINIZIONE DI

DERIVATA PRIMA

?

Come già detto nel testo di introduzione alla derivata prima, l’ obiettivo è quello di trovare l’ espressione del coefficiente angolare della retta tangente al grafico di una funzione   in un dato punto che chiameremo x₀ (il nome è legato all’ abitudine storica di chiamarlo così).

Prendiamo in considerazione la seguente figura, in cui la curva tracciata rappresenta il grafico di una certa funzione   .

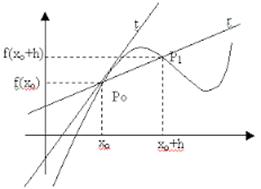
Vediamo come si può costruire la retta tangente alla funzione y = f(x) in un punto x₀ del dominio.

Consideriamo un punto   di f(x), con .

Sia P₁ un altro punto di f(x) di coordinate  con .

Cioè ci spostiamo da x₀ incrementando l’ ascissa di una quantità h > 0 e calcoliamo la corrispondente ordinata  f( x₀+h).

Avendo a disposizione due punti P₀  e P₁, siamo in grado di determinare il

coefficiente angolare m della retta   r  passante per  P₀  e P₁, che sarà una retta secante la curva:

m = .

Se immaginiamo ora di far scorrere il punto P₁ sulla curva verso il punto P₀ , l’ effetto sarà quello di far avvicinare il punto P₁ al punto P₀,  facendo ‘tendere’ la retta secante  r  alla retta tangente   t  nel punto P₀ .

In questo modo h tende a zero   ( h

Allora per ottenere il coefficiente angolare m_t della retta tangente t , bisognerà calcolare  il limite per h ®0 della quantità  m  sopra scritta.

Se  questo limite esiste ed è finito, esso sarà  chiamato DERIVATA PRIMA DELLA FUNZIONE f nel punto x₀.

m_t =

Facciamo un ulteriore passo avanti:

con questa definizione siamo in grado di conoscere la derivata prima della funzione in un punto specifico, quindi conosciamo un NUMERO.

Pensiamo invece a tale risultato come una FUNZIONE del valore x  generico variabile punto per punto

  sarà a sua volta una funzione che descrive la variazione del coefficiente angolare della retta tangente alla funzione

m_t(x) =

A QUESTO PUNTO…RICORDIAMO

quello che abbiamo già detto sul segno del coefficiente angolare di una retta  

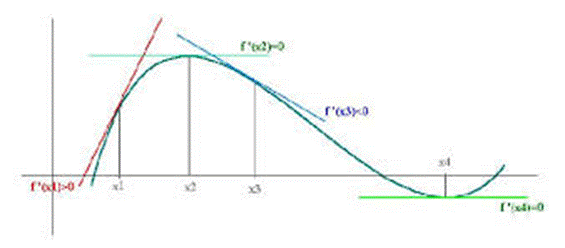
Studiare                                                                                      

· per quali valori di x si ha

· per quali valori di x si ha

· per quali valori di x si ha

sarà il prossimo obiettivo al fine di ottenere le informazioni che cerchiamo sull’ andamento del grafico della funzione.

Torna alla Home Page