DISEQUAZIONI LOGARITMICHE

Consideriamo le disequazioni logaritmiche che possiamo scrivere nella forma:

o nelle forme analoghe con gli altri segni di disuguaglianza ( ).

Per passare da una disequazione di questo tipo a una fra i due argomenti dobbiamo ricordare il comportamento della funzione logaritmica:

ü per

con

Le soluzioni di una disequazione logaritmica del tipo considerato si ottengono risolvendo il sistema formato da:

- le condizioni di esistenza dei logaritmi presenti nella disequazione

- la disequazione che si ottiene dalla disuguaglianza degli argomenti.

ESEMPIO SVOLTO n. 1

Le condizioni di esistenza sono date dalla soluzione del sistema:

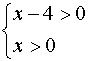
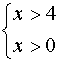
Poiché la base del logaritmo, , è minore di 1, quando si passa agli argomenti bisogna invertire il verso della disuguaglianza:

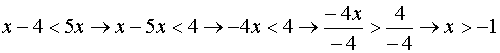
Infine, per ottenere le soluzioni della disequazione di partenza dobbiamo risolvere il sistema : 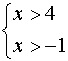quindi

ESEMPIO SVOLTO n. 2

C.E.

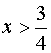
Per la definizione di logaritmo si può scrivere: 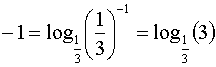, quindi la disequazione si può trasformare in da cui, essendo la base dei logaritmi minore di 1,

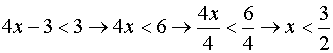
Il sistema che fornisce le soluzioni della disequazione è: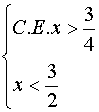

Quindi le soluzioni sono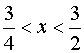

ESEMPIO SVOLTO n. 3

C.E.

Per la definizione di logaritmo si può scrivere: , quindi la disequazione si può trasformare in .

Essendo la base dei logaritmi maggiore di 1 si ha

Il sistema che fornisce le soluzioni della disequazione è: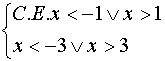

Per cui le soluzioni sono .