EQUAZIONI LOGARITMICHE
Definizione
Un’ equazione si dice logaritmica quando l’ incognita compare nell’ argomento di almeno un logaritmo.
Esempi:
![]() è un’equazione
logaritmica
è un’equazione
logaritmica
![]() NON è un’equazione logaritmica
NON è un’equazione logaritmica
Consideriamo le equazioni logaritmiche che possiamo scrivere nella forma:
![]()
dove con ![]() e
e ![]() indicano due funzioni
nell’incognita
indicano due funzioni
nell’incognita ![]() .
.
Per le condizioni di esistenza dei logaritmi
deve essere 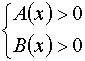
Dal momento che
![]()
![]()
![]()
per
risolvere l’ equazione è sufficiente cercare le soluzioni di ![]() e controllare successivamente
se queste soddisfano le condizioni di esistenza.
e controllare successivamente
se queste soddisfano le condizioni di esistenza.
ESEMPIO SVOLTO n. 1
![]()
Condizioni di esistenza:
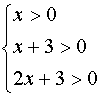
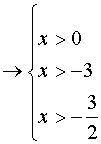
![]()
![]() cioè C.E.:
cioè C.E.: ![]() .
.
Applichiamo la proprietà del logaritmo di un prodotto:
![]()
![]()
![]()
Passando all’uguaglianza degli argomenti:
![]()
![]()
![]()
![]()
![]()
![]()
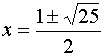 ;
; ![]()
Il valore -2 non soddisfa la condizione di esistenza posta (![]() ), che è invece
soddisfatta da 3, quindi l’ unica soluzione dell’ equazione logaritmica
iniziale è
), che è invece
soddisfatta da 3, quindi l’ unica soluzione dell’ equazione logaritmica
iniziale è ![]()
ESEMPIO SVOLTO n. 2
![]()
Le
condizioni di esistenza dei logaritmi sono date dalle soluzioni del sistema di
disequazioni 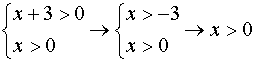 quindi
C.E.
quindi
C.E. ![]()
Applicando la proprietà del logaritmo di un prodotto al primo membro si avrà:
![]()
Il
secondo membro può essere sostituito da ![]() , in quanto il logaritmo di 10 ( in
base 10) è proprio uguale ad 1:
, in quanto il logaritmo di 10 ( in
base 10) è proprio uguale ad 1:
![]()
Ora è possibile uguagliare gli argomenti:
![]()
Questa è una semplice equazione di secondo grado che ha come soluzioni:
x1 = - 5 e x2 = +2
Considerando le condizioni di esistenza trovate prima, si vede che solo la seconda soluzione è accettabile, mentre la prima è da scartare in quanto rende negativi gli argomenti dei logaritmi.
ESEMPIO SVOLTO n. 3
![]()
Le condizioni di esistenza sono date dalle soluzioni del sistema di disequazioni
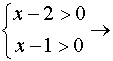
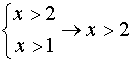 quindi C.E.
quindi C.E. ![]()
Quindi avremo:
![]()
Applicando la proprietà del logaritmo di un prodotto otteniamo:
![]()
Uguagliando gli argomenti avremo la seguente equazione equivalente:
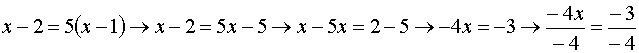
Da cui 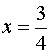 . Poiché
le condizioni di esistenza non sono soddisfatte in quanto
. Poiché
le condizioni di esistenza non sono soddisfatte in quanto ![]() , l’ equazione è IMPOSSIBILE.
, l’ equazione è IMPOSSIBILE.
Esercizi da svolgere su EQUAZIONI LOGARITMICHE

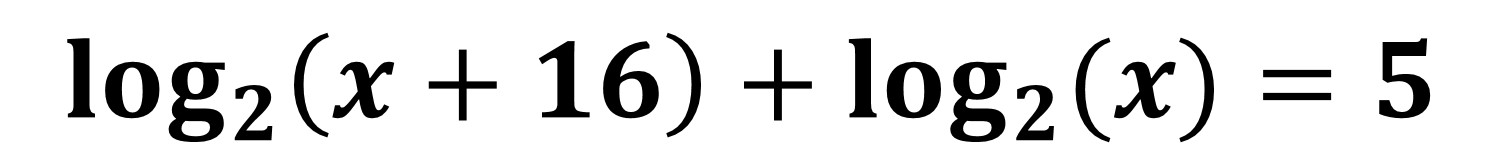 __
__

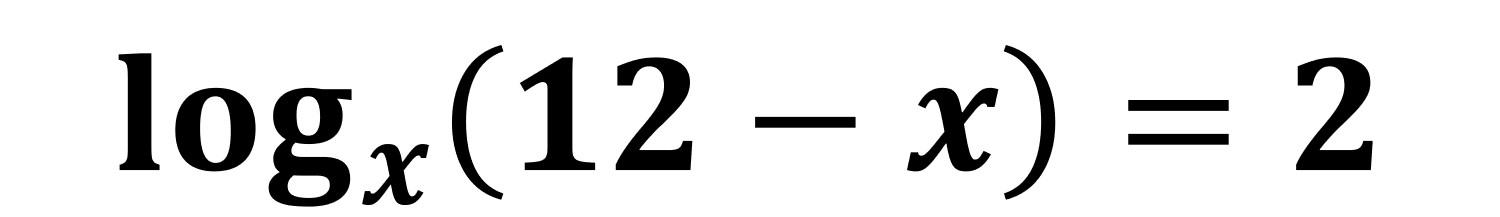

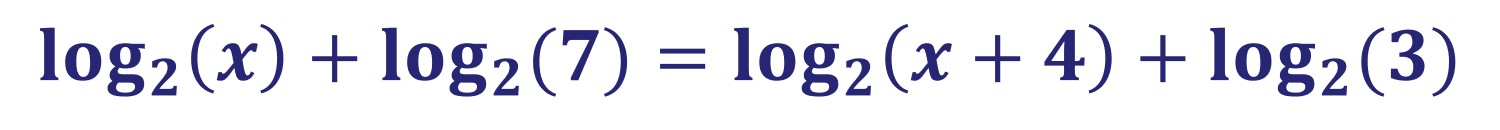 __
__

 Torna alla Home Page
Torna alla Home Page