PROTOTIPO   TEST di Matematica

1) Data la funzione   z =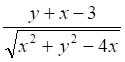

Il suo dominio è :

a) L’insieme di tutti i punti esterni alla circonferenza di centro (0;0) e raggio 2

b) L’insieme di tutti i punti interni alla circonferenza di centro (2;0) e raggio 2

c) L’insieme di tutti i punti esterni alla circonferenza di centro (2;0) e raggio 2

d) L’insieme di tutti i punti interni alla circonferenza di centro (0;0) e raggio 2

Basta imporre l’argomento della radice ≥0 … E poi si può provare a sostituire un punto qualunque appartenente all’insieme “previsto” (ad esempio P(15;0))…

Dice: ma il Punto P soddisfa anche la prima condizione….. certo !! Ma , in questo caso l’equazione della circonferenza sarebbe stata

2) Il seguente sistema di disequazioni 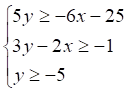   è risolto:

· a)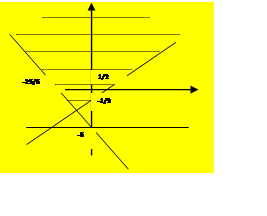   b) 

v c)      d) 

Siccome deve essere y≥-5 , la risposta non può che essere a) o c)….. anche qui sostituite un punto qualunque P(0;10) che soddisfa la condizione a) e non la c) e vedete l’effeto che fa

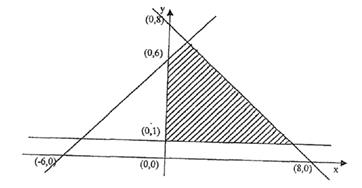
3) Considerare il dominio della  funzione .

Esso è rappresentato da tutti i punti:

□ aventi

       □ aventi

       □ aventi

      □ aventi

4) L’insieme dei punti interni alla circonferenza (e della circonferenza stessa) con centro nell’origine degli assi e di raggio 5 rappresenta:

□ l’insieme di definizione della funzione  

      □ l’insieme di definizione della funzione  

      □ l’insieme dei punti in cui la funzione    

      □ l’insieme dei punti in cui la funzione   

Solo le prime due risposte contengono l’equazione di una circonferenza come argomento della radice. Basta sostituire l’origine degli assi punto interno alla circonferenza, quindi facente parte dell’insieme delle soluzioni), e vedere che solo nel primo caso si ottiene un numero reale (radice di un numero positivo)

5) Il sistema di disequazioni 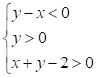è soddisfatto:

        □ in un quadrilatero                □ in una regione illimitata

        □ in un insieme vuoto             □ in due regioni illimitate              

6) Supposto che il dominio dei vincoli sia rappresentato in figura dalla parte di piano tratteggiata

                     Qual è, dei seguenti, il sistema che puoi associare a tale dominio ?

                □              □                 □                           □ 

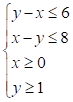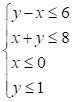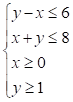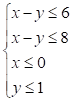
7) Il campo di esistenza delle seguente funzione in due variabili è:

             □ l’insieme dei punti del piano appartenenti al primo e al terzo quadrante, inclusi gli assi X e Y;

             □ l’insieme dei punti appartenenti al primo quadrante esclusi i semiassi cartesiani;

□ l’insieme dei punti del piano appartenenti al primo e al terzo quadrante  escluso l’asse X ed incluso l’asse Y – (0,0);

             □ l’insieme dei punti del piano appartenenti al primo e al terzo quadrante, esclusi gli assi X e Y.

8)  Considerati i punti A(2 ;-1 ;+1) e B(0 ;+3 ;-1) e l’origine degli assi, allora

 misura     □            □            □          □ 

 OB   misura    □            □              □     2          □

AO    misura     □            □              □     2          □

9) Considerato il segmento di estremi A(+3 ;-2 ;+1) e B(-3 ;+4 ;+5)  allora il punto medio M è

□   □            □          □ 

10) Considerato  il piano di equazione      , si può dire che :

a) E’ parallelo all’asse X                                   □    VERO       □    FALSO

b) E’ parallelo all’asse Z                                   □    VERO      □    FALSO

c) Passa per l’Origine                                       □    VERO      □    FALSO

d) Passa per il punto  A(5 ;-3 ;0)                     □    VERO      □    FALSO

e)  Passa per il punto B(3 ; 5 ; 24276)            □    VERO      □    FALSO

f) E’ parallelo al piano XY                                □    VERO      □    FALSO

11) Quale tra le seguenti equazioni rappresenta l’equazione di un piano passante per Q(+3 ;+1 ;-1) ? :

□              □          □        □ 

12) L’equazione  z=3 rappresenta l’equazione di…:

             □ un piano parallelo al piano XY;       □ una retta passante per A(3;3;3);

             □ asse delle z                                               □ Un piano parallelo al piano XY.