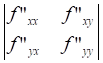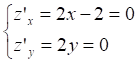Massimi e minimi di una funzione di 2
variabili con Metodo dell’Hessiano
Ricordo
che
Si
definisce MASSIMO relativo libero per una funzione z = f(x,y) un punto P0(x0,y0)
tale f(x,y) £
f(x0,y0)
per tutti i punti di un intorno di P0 contenuto
nel dominio della funzione;
si chiama invece MINIMO relativo libero
un punto P0 tale f(x,y) ³ f(x0,y0) per tutti i punti di un intorno di P0 contenuto
nel dominio della funzione.
Se
le relazioni dovessero valere non solo in un intorno di P0,
ma su tutto il dominio, allora si parla di estremanti (massimi e minimi) assoluti.
Un MASSIMO o MINIMO vincolato per una funzione di due variabili è, invece, un massimo o minimo da ricercarsi non su tutto il dominio (o su un intorno) della funzione ma all'interno del sottoinsieme del dominio che soddisfa l'equazione del vincolo, quindi ,graficamente, è il massimo o il minimo relativo della curva ottenuta dall'intersezione del dominio con la curva del vincolo di equazione g(x, y) = 0.
|
MASSIMI E MINIMI LIBERI DI UNA
FUNZIONE DI 2 VARIABILI Illustriamo, nelle linee generale, due
metodi: a) Il metodo dell'hessiano. Per
il calcolo degli estremanti liberi relativi bisogna trovare le condizioni
necessarie e sufficienti qui sotto elencate. · Si risolve il sistema: (condizione necessaria)
f'y(x,y)=0 e si trovano le coordinate dei punti critici o
stazionari tra cui gli eventuali punti di MINIMO e MASSIMO · Si calcola l'hessiano: (condizione sufficiente) H(x,y ) = · Si sostituiscono le coordinate dei punti
trovati nel risultato trovato. · Se H(x0,
y0) > 0 e f ''xx (xx, yx)<0
si ha un massimo
relativo. · Se H(x0,
y0) > 0 e f ''xx (xx, yx)>0
si ha un minimo relativo.
· Se H(x0,
y0) < 0 si ha un punto di sella. · Se H(x0,
y0) = 0 risulta un caso ambiguo e si esamina il
comportamento della funzione nell'intorno di P0 o direttamente o mediante le linee di
livello. |
Esempio:
z = x2 + y2 –2x a)
H = |