ESEMPI SVOLTI DI EQUAZIONI ABBASSABILI DI GRADO.
1) ![]() raccogliamo
raccogliamo ![]() in
evidenza
in
evidenza
![]() applicando la legge
di annullamento del prodotto, possiamo spezzare l’equazione in
applicando la legge
di annullamento del prodotto, possiamo spezzare l’equazione in
·
![]() che
ha la soluzione doppia
che
ha la soluzione doppia ![]() e
e
·
![]() che
è un’equazione di secondo grado incompleta con soluzioni
che
è un’equazione di secondo grado incompleta con soluzioni 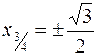
ATTENZIONE
Per risolvere ![]() non
abbiamo avuto bisogno di alcuna formula risolutiva, ci è bastato spezzarla in
due equazioni note di secondo grado mediante la fattorizzazione e la legge di
annullamento del prodotto.
non
abbiamo avuto bisogno di alcuna formula risolutiva, ci è bastato spezzarla in
due equazioni note di secondo grado mediante la fattorizzazione e la legge di
annullamento del prodotto.
2) ![]()
raccogliamo parzialmente a due a due
![]()
ora mettiamo in evidenza totale il fattore
che si ripete ![]()
applichiamo il metodo della differenza di due quadrati
![]()
ricorrendo alla legge di annullamento del prodotto possiamo spezzare l’ equazione di partenza in tre di primo grado, facilmente risolvibili
·
![]()
![]()
·
![]()
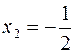
·
![]()
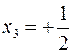
3) ![]() raccogliamo
x in evidenza
raccogliamo
x in evidenza
![]() il polinomio tra
parentesi è lo sviluppo del cubo di un binomio, quindi possiamo scrivere
il polinomio tra
parentesi è lo sviluppo del cubo di un binomio, quindi possiamo scrivere
![]()
applichiamo la legge di annullamento del prodotto
·
![]()
·
![]() ;
;
![]() ;
;
![]() contata
tre volte.
contata
tre volte.
Quindi tutte le soluzioni sono: ![]() ,
, 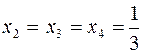
4) ![]()
tutti i metodi di scomposizione falliscono, non resta che provare con il metodo di Ruffini
![]() ß divisori del termine noto
ß divisori del termine noto
![]() ß divisori del coefficiente di grado
massimo
ß divisori del coefficiente di grado
massimo
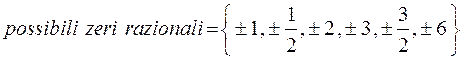
Utilizzando il teorema del resto, possiamo dire che:
![]()
cioè il polinomio A(x) è divisibile per x-1
![]()
cioè il polinomio A(x) non è divisibile per x+1
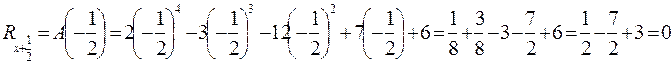
Cioè il polinomio A(x) è divisibile per x+1/2.
Abbiamo trovato due zeri del polinomio che compone l’equazione: +1 e -1/2, vuol dire che esso è divisibile per x+1 e per x+1/2 e pertanto abbassabile di due gradi, dal quarto al secondo.
|
|
|
Eseguiamo la divisione per x+1 e per x+1/2 con la regola di Ruffini. Possiamo scrivere:
|
Utilizzando la legge di annullamento del prodotto possiamo spezzare l’ equazione di quarto grado in due di primo e una di secondo che sappiamo risolvere facilmente:
·
![]() ;
;
![]()
·
![]() ;
;
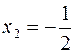
·
![]()
![]()
![]() ,
, 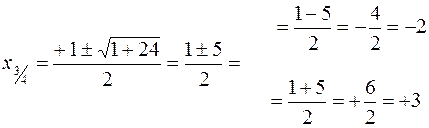
ESERCIZI PROPOSTI:
|
1)
|
2)
|
|
3)
|
4)
|
 Torna alla Home Page
Torna alla Home Page
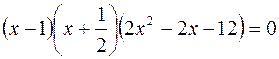 raccogliamo un 2
raccogliamo un 2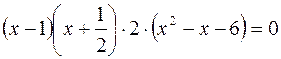 moltiplicando si ha
moltiplicando si ha