Le equazioni trinomie

Un’ equazione si dice trinomia se è composta di soli tre termini: quello di grado massimo, quello di grado metà del grado massimo e il termine noto.

La forma generale di un’ equazione trinomia è pertanto:

Più precisamente:

      equazione trinomia di 2° grado , che corrisponde all’ equazione completa di 2° grado

    equazione trinomia di 4° grado , detta anche equazione biquadratica

    equazione trinomia di 6° grado

ecc.

Per risolvere le equazioni trinomie procederemo come segue:

   prima di tutto si pone  (ricordando le proprietà delle potenze);   

sostituendo si ottiene l’ equazione ausiliaria di 2° grado ,

che risolta conduce alle soluzioni   e  ottenute applicando la nota formula .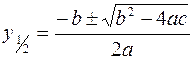

Ammesso che esistano  e , si sostituiscono i valori ottenuti nella posizione iniziale   e si ottengono due equazioni binomie di grado “n”  e .

Risolte queste otteniamo infine le soluzioni dell’ equazione trinomia di partenza.

ESEMPI SVOLTI DI EQUAZIONI TRINOMIE

Esempi risolti di equazioni trinomie di quarto grado

Torna alla Home Page