DIMOSTRAZIONE DELLA FORMULA RISOLUTIVA DELLE EQUAZIONI DI SECONDO GRADO ..

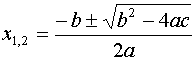
Partiamo da      .

Moltiplichiamo entrambi i membri dell’ equazione per la quantità  e otteniamo

   cioè     

Sommiamo a entrambi i membri dell’ equazione la quantità     e otteniamo

Adesso osserviamo che è possibile riconoscere al primo membro dell’ equazione il quadrato di un binomio, dato da tre dei quattro termini presenti, cioè

Isoliamo al primo membro dell’ equazione il quadrato del binomio ottenuto

    e pensando al legame esistente tra elevazione al quadrato e radice quadrata possiamo scrivere

  , quindi possiamo ricavare che 

 .

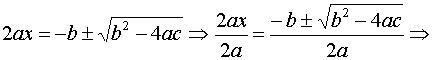
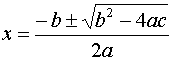In realtà è più corretto scrivere 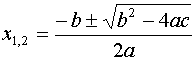in quanto le soluzioni ottenute sono DUE. Infatti, il simbolo  davanti alla radice quadrata indica che si ha

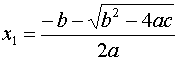
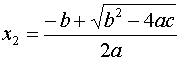
Quale idea c’è dietro questa dimostrazione? Cioè perché fare proprio quelle scelte sulle quantità da moltiplicare o aggiungere? A quale scopo?

A partire dal testo si punta a ‘scovare’ quei numeri che riescono a far ‘apparire’ un quadrato di binomio!

Proviamo con un esempio…

consideriamo l’ equazione   .

Osserviamo che   è già in parte il quadrato di un binomio; ci servirebbe + 4 per completare l’ opera…allora perché non scrivere +4 – 9 anziché – 5 ? Cioè   …E senza bisogno di magia, ma solo di aritmetica!

Quindi si ha    , che corrispondono a due equazioni di primo grado, cioè  

  e   .

Per cui le soluzioni sono:      e     .

La dimostrazione che abbiamo visto con  e  non è altro che la generalizzazione di un caso particolare.

Potevamo partire da un altro caso particolare, ma la strada sarebbe stata simile, sempre alla ricerca di un quadrato di binomio…

A furia di provare casi particolari si è trovata la struttura generale delle quantità che rispondevano alla richiesta…ed ecco la dimostrazione della formula generale.

Torna alla Home Page