DISTANZA  TRA DUE PUNTI  A E B  DEL  PIANO  CARTESIANO

La distanza tra due punti A e B del piano cartesiano non è altro che la lunghezza del segmento AB che li unisce.

In questa situazione le coordinate cartesiane dei punti A e B sono note,

quindi supponiamo che  e  . Le coordinate di H saranno pertanto .

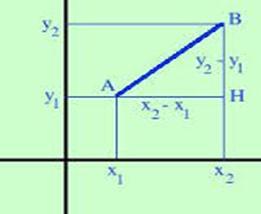
Ragionando sul triangolo ABH, rettangolo in H, e applicando a questo triangolo il teorema di Pitagora si ottiene:

Esercizi svolti applicando il teorema di Pitagora

AB =   = 

Facciamo un esempio:

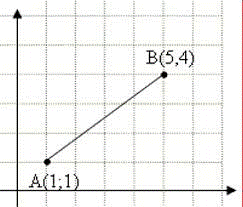   Secondo quanto dimostrato sopra possiamo applicare direttamente la formula ottenuta sostituendo i dati:

AB =

Avremmo potuto anche scegliere come primo punto di cui sostituire le coordinate cartesiane A, scrivendo:

AB =

SI OTTIENE OVVIAMENTE  LO STESSO RISULTATO!

NON IMPORTA QUALE DEI DUE PUNTI SI SCEGLIE PER PRIMO NELLA SOSTITUZIONE DEI DATI, LA COSA IMPORTANTE E’

MANTENERE LO STESSO ORDINE

SIA PER LA X CHE LA Y DEI DUE PUNTI.

Torna alla Home Page