DISEQUAZIONI FRATTE e DISEQUAZIONI IN CUI IL PRIMO MEMBRO è UN POLINOMIO SCOMPONIBILE IN FATTORI

 

                                   

 

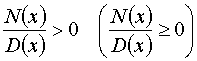
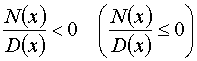
Poiché risolvere una disequazione fratta significa individuare tutti i valori della variabile  che rendono negativa (in caso di disuguaglianza di minoranza “< 0”) o rendono positiva (in caso di disuguaglianza di maggioranza “> 0” ) la frazione,

 

prima studiamo separatamente il segno del numeratore e quello del denominatore

 

ü Indipendentemente dal verso della disuguaglianza si pone:

 

 

   

   ATTENZIONE !

Per il denominatore non si pone mai     , in quanto anche se nella disequazione fratta è presente il segno di    , il denominatore non può mai assumere valore = 0, altrimenti la frazione algebrica perderebbe di significato.

 

ü    Si rappresentano graficamente i segni del numeratore e del denominatore e, nei singoli intervalli che si formano:

ü     Si ricava il segno del quoziente con la regola dei segni della divisione

ü si prenderanno gli intervalli in cui si ottiene “+” se la disequazione fratta voleva le soluzioni “> 0”

ü si prenderanno gli intervalli in cui si ottiene “-” se la disequazione fratta voleva le soluzioni “< 0”

 

Per la rappresentazione grafica delle disequazioni useremo sempre le seguenti convenzioni:

 

·        La linea continua per rappresentare la zona in cui la disequazione è verificata

 

·        La linea tratteggiata per rappresentare la zona in cui la disequazione non è verificata

 

Osservazione importante

 

Se la disequazione fratta non è ridotta in forma canonica, cioè se non abbiamo una sola frazione algebrica al 1° membro, allora bisogna portare prima tutto a 1° membro, eseguire il m.c.m. dei denominatori, eseguire tutte le operazioni al numeratore e successivamente procedere allo studio del segno del numeratore e denominatore.

(Qui forse ci starebbe bene un link con le operazioni con le frazioni algebriche)

 

Si risolvono allo stesso modo anche le disequazioni che al 1° membro hanno un polinomio che si può scomporre in fattori, facendo il GRAFICO DEL SEGNO DEI FATTORI, e calcolando il segno del prodotto nei diversi intervalli che si formano.

 

ESEMPI SVOLTI

 

1) 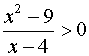         Studiamo il segno del numeratore e quello del denominatore:

 

    Consideriamo l’ equazione associata    , la quale ammette due soluzioni opposte   . Allora per la disequazione avremo le soluzioni .

 

 

Mettendo insieme le due situazioni possiamo determinare il segno del quoziente:

 

 

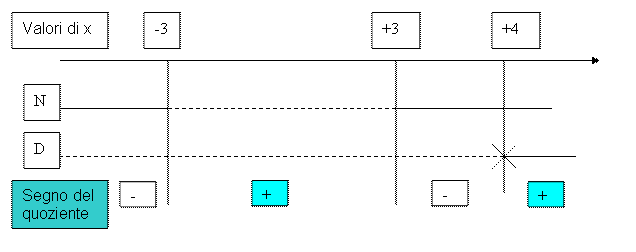
Le soluzioni della disequazione iniziale saranno quindi    

 

La croce sul valore 4 sta ad indicare che tale valore non può essere preso in considerazione perché annullerebbe il denominatore della frazione.

 

ü IMPORTANTE

 

Osserviamo che la disequazione     ha le stesse soluzioni della precedente proprio perché il segno di un quoziente e il segno di un prodotto sono dati dalle stesse regole!

 

2) 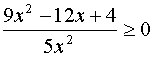      Studiamo il segno del numeratore e del denominatore:

 

N:                     in quanto se 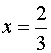  è verificato il segno di = , per tutti gli altri valori di x è verificato il segno di >.

 

D:            

 

Anche se nella disequazione fratta c’è il   studiamo soltanto il > 0 perché, come abbiamo detto precedentemente, altrimenti la frazione perderebbe di significato.

 

Riportiamo i risultati ottenuti nel grafico per determinare il segno del quoziente:

 

Valori di x

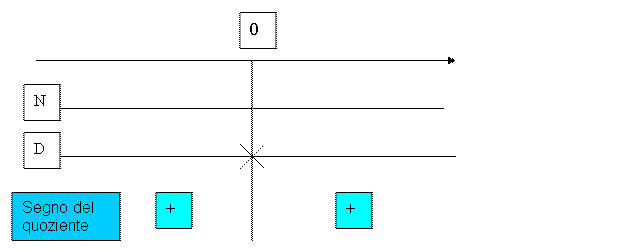
Quindi le soluzioni della disequazione fratta sono:  

 

3) 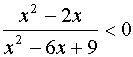       Studiamo il segno del numeratore e del denominatore:

 

N:        L’ equazione associata ammette due soluzioni distinte:

 

  Per la legge di annullamento del prodotto abbiamo quindi le soluzioni      e    . La disequazione è allora verificata per .

 

D:             

 

Riportiamo i risultati ottenuti nel grafico per determinare il segno del quoziente:

 

 

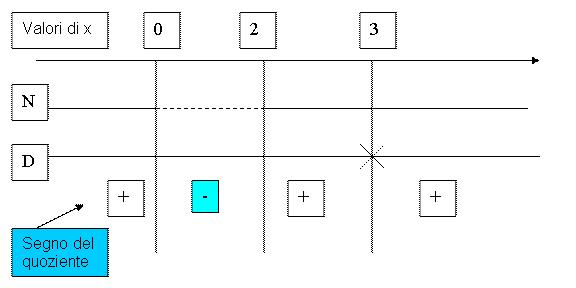
Poiché la disequazione iniziale chiedeva < 0, le soluzioni saranno quelle corrispondenti all’ intervallo in cui abbiamo ottenuto il segno del quoziente negativo, cioè:   .

 

 

4)  

 

Qui siamo nel caso di una disequazione intera in cui il primo membro è un polinomio che può essere fattorizzato e per il quale poi potremo studiare il segno del prodotto dei suoi fattori.

Cominciamo a scomporre il polinomio mediante il raccoglimento parziale dei fattori comuni:

 

 

Quindi la disequazione può essere scritta come segue:  

Allora studiamo il segno dei singoli fattori:

 

1° FATTORE:      

L’ equazione associata ammette le seguenti soluzioni:                 .  Quindi la disequazione è verificata per   .

 

2° FATTORE:               .

 

Riportiamo i risultati ottenuti nel grafico per determinare il segno del prodotto:

 

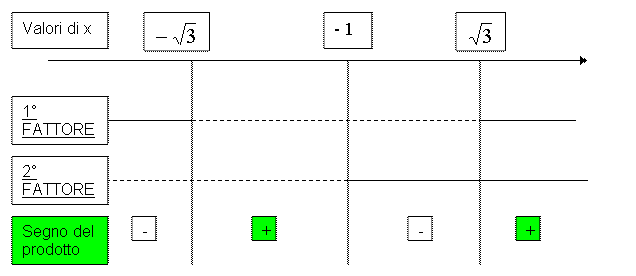
Quindi le soluzioni della disequazione iniziale saranno: , in quanto è proprio in questi intervalli di valori che abbiamo ottenuto il segno positivo del prodotto.

 

ü IMPORTANTE

 

Se avessimo la disequazione     ,  che differisce da quella appena risolta soltanto per il verso della disuguaglianza, l’ unica differenza nel procedimento di risoluzione sarebbe alla fine, quando dal grafico del segno del prodotto prenderemmo come soluzioni gli intervalli di valori di x in cui c’è il segno - , cioè :   .

 

 

Bisogna rendersi conto del fatto che per riuscire a risolvere una disequazione di questo tipo è necessaria una buona conoscenza dei metodi per la scomposizione di un polinomio!

     Tutto è collegato!         

L’ algebra di base è necessaria per andare avanti con argomenti più complessi.  Per costruire un puzzle sono necessari tutti i pezzi!  

Video - Esercizi risolti: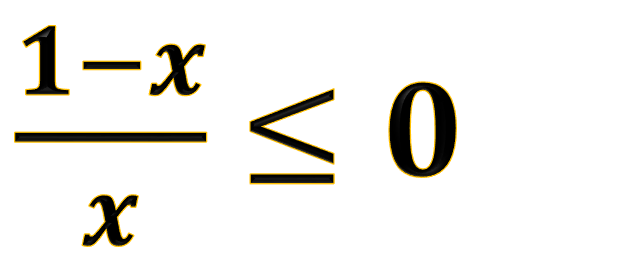

 

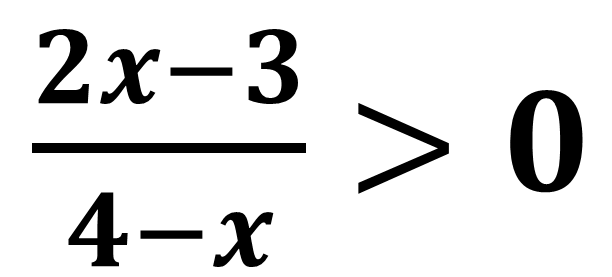
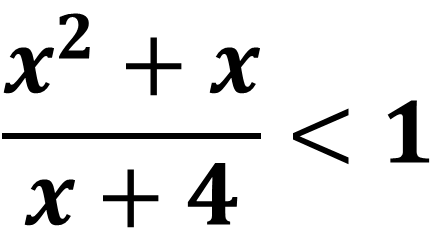
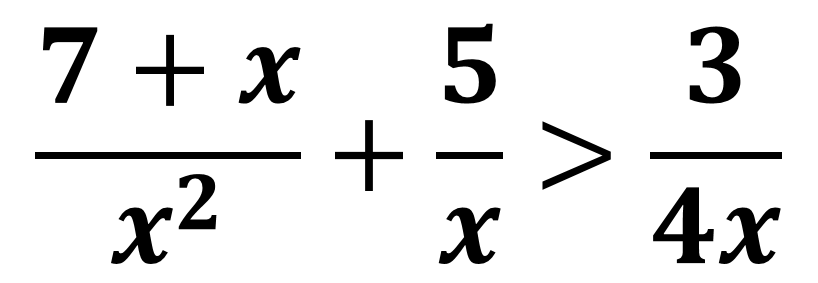
ESERCIZI PROPOSTI

Torna alla Home Page