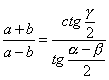FORMULARIO: goniometria

DEFINIZIONI

» FUNZIONI GONIOMETRICHE
  ,    

» FUNZIONI INVERSE
,   ,   

» LIMITAZIONI
   ,  

» RELAZIONE FONDAMENTALE DELLA GONIOMETRIA

» SIGNIFICATO GEOMETRICO DELLE FUNZIONI GONIOMETRICHE

	sen α = PQ cos α = OQ tg α = AT ctg α = BR
Muovi il punto P per vedere come variano le lunghezze dei segmenti orientati.

ESPRESSIONE DI TUTTE LE FUNZIONI GONIOMETRICHE DI UN ANGOLO ORIENTATO MEDIANTE UNA SOLA DI ESSE
NOTO

ARCHI ASSOCIATI
ANGOLI COMPLEMENTARI	ANGOLI CHE DIFFERISCONO DI UN ANGOLO RETTO
ANGOLI CHE HANNO PER SOMMA TRE ANGOLI RETTI	ANGOLI CHE DIFFERISCONO DI TRE ANGOLI RETTI
ANGOLI CHE DIFFERISCONO DI UN ANGOLO PIATTO	ANGOLI SUPPLEMENTARI
ANGOLI ESPLEMENTARI	ANGOLI OPPOSTI
FORMULE DI ADDIZIONE E SOTTRAZIONE
FORMULE DI DUPLICAZIONE
FORMULE DI BISEZIONE
,      ,
FORMULE PARAMETRICHE
,      ,
FORMULE DI WERNER
FORMULE DI PROSTAFERESI
FORMULE DI BRIGGS
, , , , , , , ,
FORMULE DI NEPERO
,

FUNZIONI GONIOMETRICHE DI ANGOLI PARTICOLARI
Gradi	Radianti	sen	cos	tg	ctg
0°	0	0	1	0	non esiste
30°
45°				1	1
60°
90°		1	0	non esiste	0
180°		0	-1	0	non esiste
270°		-1	0	non esiste	0
360°		0	1	0	non esiste

---

	FORMULARIO: trigonometria. Risoluzione dei triangoli
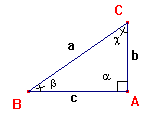
» Risoluzione dei triangoli rettangoli.
	1° Teorema In un triangolo rettangolo, la misura di un cateto è uguale al prodotto della misura dell’ipotenusa per il seno dell’angolo opposto oppure per il coseno dell’angolo adiacente. , ,
	2° Teorema In un triangolo rettangolo, la misura di un cateto è uguale a quella dell’altro cateto per la tangente dell’angolo opposto al primo, o per la cotangente dell’angolo adiacente. , ,
» Area di un triangolo qualsiasi.
L’area di un triangolo qualsiasi è uguale al semiprodotto delle misure di due suoi lati per il seno dell’angolo fra essi compreso.
» Risoluzione dei triangoli qualsiasi.
Teorema dei seni (o di Eulero) In un triangolo qualunque è costante il rapporto tra la misura di un lato e il seno dell’angolo opposto: Nota. La costante è la misura del diametro della circonferenza circoscritta, per cui è possibile enunciare il seguente: Teorema della corda In un triangolo il rapporto tra la misura di un lato e il seno dell’angolo opposto è uguale al diametro della circonferenza circoscritta: = 2r	Teorema del coseno (o di Carnot) In un triangolo qualsiasi il quadrato di un lato è uguale alla somma dei quadrati degli altri due diminuita del doppio prodotto di questi due lati per il coseno dell’angolo fra essi compreso: Nota. Il teorema di Carnot generalizza il Teorema di Pitagora, a cui si riduce se si considera un triangolo rettangolo.	Teorema delle proiezioni In un triangolo qualunque, la misura di un lato è uguale alla somma dei prodotti delle misure di ciascuno degli altri due per il coseno degli angoli che essi formano con il primo:
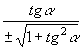
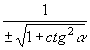
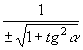
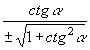
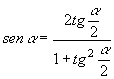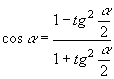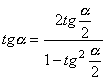
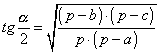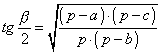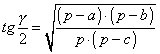
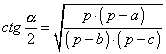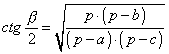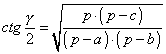
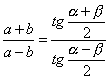IN PRATICA Per risolvere un triangolo qualsiasi devono essere noti tre elementi di cui almeno un lato. Dunque si possono presentare quattro casi: 1) due angoli e un lato (il problema presenta una sola soluzione) 2) tre lati (il problema presenta una sola soluzione) 3) due lati e l’angolo compreso (il problema presenta una sola soluzione) 4) due lati e un angolo opposto ad uno di essi (il problema può avere nessuna, una o due soluzioni).

Torna alla Home Page