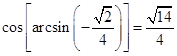Proviamo a costruire la funzione inversa di sin y , cioè la funzione che, dato un valore del seno associa il corrispondente valore dell’angolo. Tale funzione si chiama arcoseno e si scrive

che significa “x è l’angolo il cui seno è y”. Si conviene però di assumere per x solo gli angoli compresi tra  e , cioè .

Analogamente si può definire la funzione inversa della funzione , se si considerano solo angoli appartenenti all’intervallo chiuso . Essa si chiama arcocoseno e si scrive

che significa “x è l’angolo il cui coseno è y”.

In modo analogo dalla funzione , se si considerano solo angoli appartenenti all’intervallo aperto , si può ricavare la funzione inversa. Tale funzione si chiama arcotangente e si scrive

che significa “x è l’angolo la cui tangente è y”.

Esempio: calcoliamo il valore di .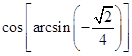

Poniamo 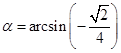. Vogliamo dunque calcolare il coseno di un angolo  sapendo che il seno è . Possiamo applicare la prima equazione fondamentale della goniometria e otteniamo:

.

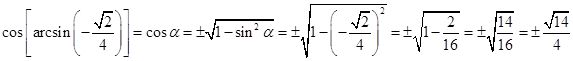Per quanto si è detto prima però la funzione arcoseno è definita soltanto per angoli , e per tali angoli il coseno è positivo, quindi tra i due valori  dobbiamo prendere solo quello positivo. In definitiva abbiamo

Torna alla Home Page