Relazioni tra particolari coppie di angoli
Angoli associati
Si costruisca al solito modo una
circonferenza goniometrica e si consideri un angolo orientato ![]() come in figura. Sia B il
punto della circonferenza goniometrica associato ad
come in figura. Sia B il
punto della circonferenza goniometrica associato ad ![]() .
Dal punto B si conduca la parallela all’asse delle ascisse e sia
.
Dal punto B si conduca la parallela all’asse delle ascisse e sia ![]() il punto in cui tale parallela
incontra la circonferenza; si conducano poi i diametri
il punto in cui tale parallela
incontra la circonferenza; si conducano poi i diametri ![]() e
e ![]() .
Risultano in tal modo individuati gli angoli
.
Risultano in tal modo individuati gli angoli
![]()
![]()
![]()
che si chiamano angoli associati all’angolo dato ![]() .
.
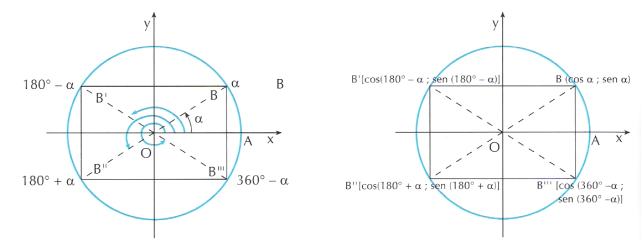
Vogliamo determinare il seno, il
coseno e la tangente degli angoli associati ad ![]() .
Analizzando la figura si ha:
.
Analizzando la figura si ha:
![]() Angoli supplementari:
Angoli supplementari: ![]() e
e
![]()
![]()
![]()
![]()
![]()
![]() Angoli che differiscono di 180°:
Angoli che differiscono di 180°: ![]() e
e ![]()
![]()
![]()
![]()
![]()
![]() Angoli esplementari:
Angoli esplementari: ![]() e
e
![]()
![]()
![]()
![]()
![]()
Angoli opposti
Due angoli si dicono opposti se la loro somma è zero.
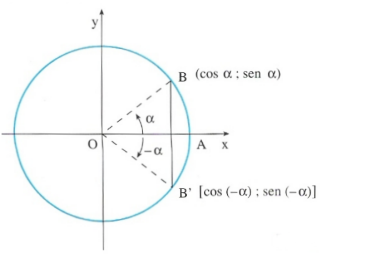
Tali angoli possono essere considerati come due angoli orientati in senso opposto e la cui ampiezza è uguale in valore assoluto. I loro rispettivi punti associati sulla circonferenza goniometrica B e B coincidono con i punti associati a due angoli esplementari. Si avrà allora:
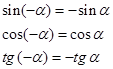
Angoli complementari
Due angoli si dicono complementari se la loro somma è 90°. Consideriamo
in figura gli angoli ![]() e
e ![]() .
.
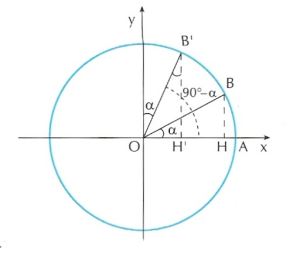 I triangoli OBH
e
I triangoli OBH
e ![]() sono congruenti poiché sono
rettangoli in H e
sono congruenti poiché sono
rettangoli in H e ![]() , hanno
, hanno ![]() e
e ![]() .
I lati corrispondenti in triangoli congruenti sono congruenti, quindi si avrà:
.
I lati corrispondenti in triangoli congruenti sono congruenti, quindi si avrà:
![]()
![]()
![]()
![]()
Si avrà poi:
![]()
![]()