Modelli lineari: un esempio.

Il seguente esempio rientra tra i modelli lineari, cioè tra i modelli matematici di un fenomeno che sono descritti mediante funzioni lineari.

Caduta di un grave
Il baricentro di un corpo è soggetto alla forza di gravità che, in prossimità della superficie terrestre, agisce imponendo ai corpi una accelerazione costante, verticale e diretta verso il basso g=9.8m/s².
In assenza di altre forze e trascurando la resistenza dell’aria, la velocità (variabile dipendente) di un corpo in caduta libera varia nel tempo (variabile indipendente) secondo la legge:

dove v₀ è la velocità iniziale del corpo.

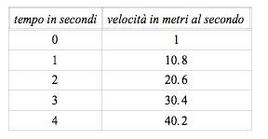
Tabella 1.1: Velocità del grave in funzione del tempo.

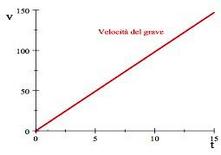
Figura 1: Grafico della velocità.

---

Informazioni sul fenomeno
Un corpo che cade nel vuoto non ha velocità costante, ma la sua velocità aumenta con il tempo (vedi Tabella 1.1 e Figura 1 in cui v₀=0)

Previsioni sul fenomeno
Ad ogni istante t è nota la velocità del corpo in quell’istante.
Ad esempio, se inizialmente risulta v₀=0 è possibile determinare la velocità del corpo dopo 10s senza eseguire materialmente alcun esperimento:

v(10s)=9.8m/s²·10s=98m/s.

Controllo del fenomeno
Se si vuole che il corpo dopo 15s raggiunga la velocità di 150m/s quanto dovrà valere la velocità iniziale v₀?

In altre parole, per ottenere dopo 15s il valore di 150m/s dobbiamo imprimere al corpo una velocità iniziale di 3m/s.

Limiti di validità del modello
Questo modello non è adatto alla descrizione del moto di un paracadutista o alla progettazione di un paracadute, poiché trascurando la resistenza dell’ aria nel modello non rimane traccia della forza resistente del mezzo che si oppone al moto e che dipende dalla velocità del corpo e dalle sue caratteristiche geometrico-materiali.

Torna alla Home Page