Un modello matematico è una descrizione in termini

 matematici, cioè mediante funzioni, equazioni,…, di un

fenomeno reale ed è in grado di descrivere i legami esistenti tra

 le grandezze caratteristiche del fenomeno.

Ad esempio, i modelli matematici sono utilizzati per la descrizione della numerosità di una popolazione di individui, della velocità di un oggetto in caduta libera, della concentrazione di un reagente in una reazione chimica, dell’aspettativa di vita di una persona alla nascita, etc.

Come si costruisce un modello matematico?

Cerchiamo si spiegarlo…

Fase 1: Analisi del problema reale: ipotesi e dati sperimentali
Questa prima fase di analisi di un problema reale deve condurre all’individuazione degli aspetti essenziali del fenomeno che si intende modellizzare. Se le ipotesi sul fenomeno e l’ analisi dei dati sperimentali conducono a stabilire l’ esistenza di relazioni evidenti tra le quantità che sono essenziali per la sua descrizione, allora è possibile individuare le variabili indipendenti e quelle dipendenti che intervengono nel fenomeno e ipotizzare un possibile legame funzionale. Naturalmente, può essere necessario fare delle assunzioni che semplifichino la struttura del fenomeno in modo da renderlo matematicamente trattabile. D’ altra parte, se si tentasse una descrizione della realtà pretendendo di tener conto di tutti gli aspetti del fenomeno, il modello sarebbe così complicato da risultare del tutto inutilizzabile.

Fase 2: Formulazione del modello matematico

Con le conoscenze acquisite sull’ andamento del fenomeno si possono ottenere delle funzioni o delle equazioni che correlino le diverse variabili. Se però non si può far riferimento ad alcuna conoscenza fisica a priori che possa fungere da traccia, occorre raccogliere ed esaminare un buon numero di dati sperimentali in modo da ottenerne una rappresentazione grafica e da discernere se questa descrizione del fenomeno presenti un andamento o una forma peculiare. Il grafico può in effetti suggerire quale “formula matematica” è più adatta a descrivere il fenomeno.

Fasi 3–4: Risoluzione del modello matematico e previsioni sul fenomeno
Formulato il modello, è necessario applicare teorie e tecniche matematiche in grado di risolvere il complesso di funzioni o equazioni che reggono il modello al fine di ricavare delle informazioni sul fenomeno, di interpretare in chiave fisico-sperimentale queste informazioni facendo anche delle previsioni sull’andamento futuro del fenomeno.

Fase 5: Validazione del modello matematico
Se la descrizione del fenomeno e le previsioni future dedotte dal modello non combaciano con l’ evidenza sperimentale, è necessario ridefinire il modello e incominciare un nuovo ciclo. In questo caso, è evidente che o non si sono individuate al meglio le grandezze caratteristiche del fenomeno oppure le ipotesi sui legami funzionali non sono corrette.

Obiettivi di un modello matematico
Un modello matematico deve servire a comprendere meglio il fenomeno in esame, a fornire previsioni sul suo andamento futuro e ad operarne un controllo.

Un modello matematico non è mai una rappresentazione esatta della realtà.

Un modello matematico semplifica “sufficientemente” la realtà, ma, nei limiti di validità del modello, cioè quelli imposti dalle dovute semplificazioni, è estremamente accurato nella descrizione e nelle previsioni future sul fenomeno in esame.

Schema per la costruzione di un modello matematico

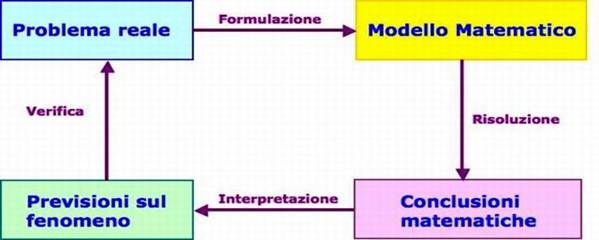
Per curiosità… Esempio di modello lineare

Torna alla Home Page