La goniometria si occupa dello studio degli angoli.
Angoli e loro misure
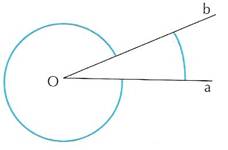
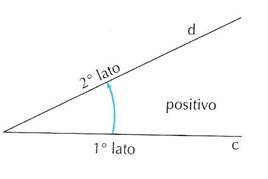
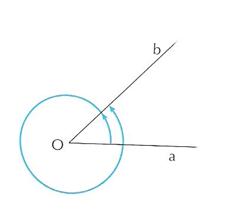
Considerate in un piano due semirette a,b di origine O. Si definisce angolo ciascuna delle due parti del piano delimitate dalle due semirette (quindi sia quella interna sia quella esterna)
Il punto O è il vertice e le due semirette lati
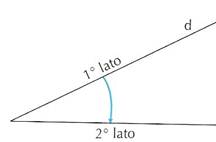Un angolo si dice orientato quando si stabilisce quale dei due lati
è il primo e quale il secondo.
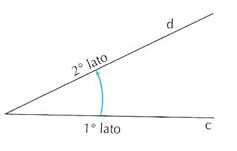
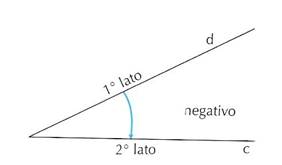
si considera positivo un angolo che si ottiene con una rotazione antioraria, negativo un angolo che si ottiene con una rotazione oraria.
Nello studio di alcune discipline, però, tra le quali la Topografia, è vero il contrario, perché si usano degli strumenti che “leggono” gli angoli in modo “orario”
Angoli Particolari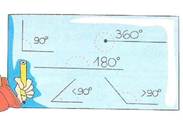 
Il sistema
sessagesimale 
Il sistema
radiale 
Da gradi a radianti
Da radianti a gradi
Rivediamo le proprietà delle proporzioni
Ora che sappiamo risolvere anche le equazioni, guardiamo questo metodo efficace per trovare la frazione generatrice di un numero periodico
A quale frazione corrisponde un dato numero periodico
può ritornare utile quando, dovendo passare da gradi a radianti, ci troviamo di fronte, per l'appunto, ad un numero periodico
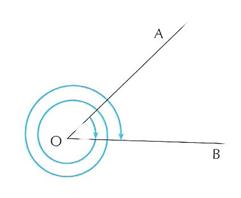
Angoli impropri
Consideriamo l’angolo 
di lati a,
b e di vertice o. Tale angolo è descritto dalla rotazione del
primo lato a sul secondo lato b.
|
|
Osserviamo che il lato a può sovrapporsi al lato b anche dopo aver descritto un numero qualsiasi di angoli giri.
Gli angoli che si ottengono da un
angolo sommato
ad un certo numero di angoli giri, si chiamano angoli
impropri.
In generale, se 
è l’ampiezza di
un angolo di lati a e b, tutti gli angoli aventi gli stessi lati,
espressi in gradi, sono:
dove k è un intero
relativo che indica il numero di giri completi che la semiretta a compie
attorno al vertice o dopo aver descritto l’angolo di ampiezza . L’intero k
è positivo o negativo a seconda che la semiretta a compia i giri completi
in senso antiorario o in senso orario.
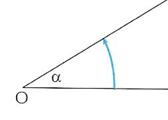
La circonferenza goniometrica Consideriamo in un piano
cartesiano xOy la circonferenza con il centro nell’origine e raggio pari
ad uno. Tale circonferenza si chiama circonferenza
goniometrica. In figura 3 sono riportati i
punti associati agli angoli particolari. Il punto A è associato
all’angolo di 0° e anche all’angolo di 360°; il punto B è associato
all’angolo retto; il punto C all’angolo piatto; il punto D è
associato all’angolo di 270°.
Figura 3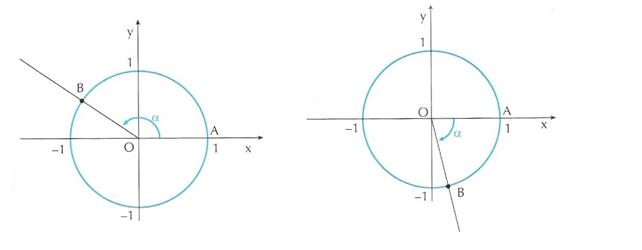
Sia dato un angolo
orientato .
Disponiamo tale angolo nel piano cartesiano nel seguente modo: facciamo
coincidere il vertice dell’angolo con l’origine O del sistema di
riferimento e il suo primo lato con il raggio OA. Sia B il punto in cui
il secondo lato dell’angolo interseca la circonferenza. Qualunque sia l’angolo il punto A viene
a trovarsi sempre nella stessa posizione e quindi ha sempre le stesse
coordinate: A(1,0); la posizione di B invece, dipende dall’angolo
scelto. Chiamiamo B il punto associato
all’angolo sulla
circonferenza goniometrica.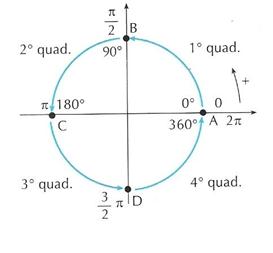
Seno e coseno di
un angolo
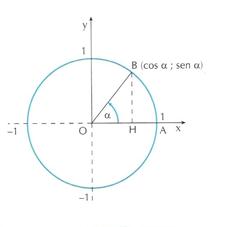
Si dice seno di un angolo l’ordinata del punto associato ad nella
circonferenza goniometrica. (in figura il seno di è BH)
Si dice coseno di un angolo l’ascissa del punto associato ad nella
circonferenza goniometrica. (in figura il coseno di è OH)
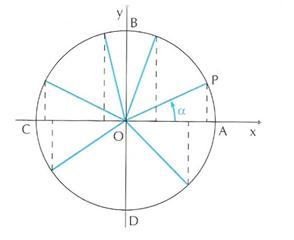
Consideriamo adesso l’angolo di figura 4 e
supponiamo che il punto P si muova sulla circonferenza in modo che
l’angolo assuma
tutti i valori possibili tra 0° e 360°.
|
Quando 
, cioè 
, l’ordinata di P è
zero e l’ascissa di P è uno, quindi si avrà:
; 
.
Se P si sposta da A
a B nel primo quadrante, cioè cresce da 0° a 90°, l’ordinata di P
è positiva, cioè 
, e cresce da 0 a 1, mentre l’ascissa
di P è positiva, cioè 
, ma decresce da 1 a 0.
Si avrà poi quando 
; 
.
Se si osserva attentamente la
figura 4, si ottiene che al crescere di da 90° a 180°, nel secondo
quadrante, è e 
decresce da 1 a 0, mentre 
e 
decresce da 0 a
–1.
Quando 
si ha
; 
.
Al crescere di da 180° a 270°
nel terzo quadrante, il seno decresce da 0 a –1 ed è negativo, mentre il
coseno cresce da – 1 a 0 ed è negativo.
Quando 
si avrà
; 
.
Al crescere di da 270° a 360°,
nel quarto quadrante, il seno cresce da – 1 a 0 ed è negativo, mentre il
coseno cresce da 0 a 1 ed è positivo.
A questo punto, quando P torna in A, si ha
; 
.
Crescendo oltre 360° i valori del
seno e del coseno si ripetono periodicamente; diremo quindi che il seno ed il
coseno sono funzioni periodiche con periodo uguale a 360° e si scrive:
; 
.
dove k è un qualsiasi numero intero positivo o negativo.
Se per misurare l’angolo si utilizzano i
radianti, si scrive:
; 
.
Tangente di un angolo
Sia dato un angolo ; costruiamo al
solito modo la circonferenza goniometrica e conduciamo dal punto A la
retta t tangente alla circonferenza. Sia T il punto in cui il
secondo lato dell’angolo, o il suo prolungamento, incontra tale tangente.
In figura si vede come cambia la
situazione se appartiene
al primo, secondo, terzo, o quarto quadrante.
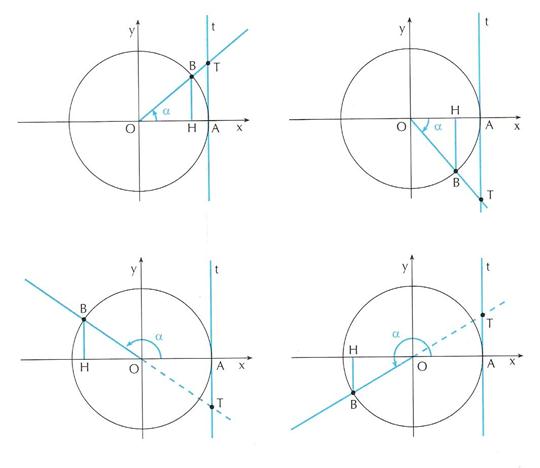
La tangente di un angolo orientato è l’ordinata del punto di intersezione tra il secondo lato dell’angolo, o il suo prolungamento, con la retta tangente alla circonferenza goniometrica nel punto A.
Si osservi che se il secondo lato
dell’angolo viene
a cadere sull’asse y, tale lato risulta parallelo alla retta t, e
quindi non può mai intersecarla.
Perciò se 
, la tangente di non esiste.
Mentre se , il punto T
coincide con il punto A, pertanto la sua ordinata è zero. Risulta quindi
Anche per 
il punto T coincide
con A, quindi
Anche la tangente, come il seno ed il coseno, è una funzione periodica, ma stavolta il periodo non è un angolo giro, ma un angolo piatto. La tangente di un angolo, cioè, assume gli stessi valori ogni 180°. Scriveremo quindi
oppure 
Relazioni
fondamentali della trigonometria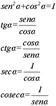
Valore di
funzioni trigonometriche di angoli particolari 
Le funzioni
inverse 
Relazione
tra particolari coppie di angoli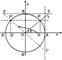 
Formulario
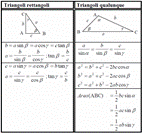
Il
grafico di funzioni trigonometriche
Torna alla Home Page